This summer, Rory and I spent our rest hour at the cottage doing a few school-related activities: Reading, Writing and Arithmetic! When we had guests, they were always intrigued by the ‘weird way’ Rory was doing his addition and so I spent my summer convincing my friends and family that, delaying the algorithm is actually a better way to learn how to add two digit numbers! Let’s see if I can make you a believer too!

“For addition and subtraction, well-understood and practiced invented strategies are sometimes more efficient and often more accurate (than standard algorithms).” Van de Walle

Why is delaying the algorithm a better way to learn?

1. The algorithm is digit-oriented; we want addition to be number oriented! This means children will see 43+36 as 40+30 and know that the answer will be close to 70. Teaching to add 4+3 (the algorithm) not only un-teaches place value, but students aren’t able to check for reasonableness of their answer (is it 7?!).
2. The algorithm is right-handed; but children are familiar with reading left to right. Adding left to right also emphasizes the size of the answer, thus reinforcing place value.
3. Children make fewer errors and less reteaching is required, when you don’t force an algorithm. This is because it makes sense (with a good understanding of place value). Teaching to ‘carry your ones’ and ‘start from the right’ are rules that don’t make sense, especially to struggling students; but grouping your tens and your ones (i.e. like terms) makes sense!
4. Decomposing numbers is the basis for mental computation and estimation. Try it: add 74+38 in your head. How did you do it? Did you ‘carry your one’?! Probably not. You probably did 70+30 is 100 and 8+4 is 12 more so 112. Even if you started with 8+4…I doubt you carried the one and tried to picture it in your head. If you did….try a 3-digit number and see what happens!
5. Thinking flexibly and having different strategies helps build number sense. An algorithm doesn’t allow for this flexibility.

Learning to Add Two-Digits

Two-digit addition normally pops up in Grade 2. The first iterance should be with manipulatives such as ten frames, 100 charts, counters, place value cards, cuisenaire rods, and base 10 blocks. It should also be embedded in problem-solving and introduced in an authentic and meaningful way. It is only once students are confident with the concept and can solve problems concretely, and pictorially, that you are ready to present how to solve these problems abstractly.

Once your students are ready, here are the steps to begin:

A. Place Value

First and foremost, your child needs to be comfortable with place value.  This isn’t just the ability to read a number with two digits properly; it is demonstrating an understanding that the first digit represents how many tens (46 = 4 tens) and the second digit represents how many ones (46=6 ones). Here are some other posts on place value: The Importance of Place Value in Primary, Digits versus Numbers, Place Value Activities.

B. Decomposing numbers

Your child needs to be confident decomposing numbers. In other words, they should understand that 31 = 30+1, or 47=40+7. Place value cards are a great way to teach both place value and decomposing numbers. Once your student is extremely able to break apart numbers, you are ready to add abstractly in a way that makes sense!

C. Addition without regrouping

Van de Walle talks a lot about invented strategies. Since you will have already spent some time doing double digit addition concretely, your students will have already formulated methods to add numbers abstractly. By starting with ‘easy’ questions that don’t require bridging 10 or regrouping, students will see the link between grouping tens and grouping ones. Continue to work with place value cards until the student is confident enough to do it without. 

D. Addition with regrouping

DO NOT TEACH THE ALGORITHM FIRST! Instead, show the numbers with place value cards first, and use the cards to decompose the numbers horizontally, like the picture above.  Then allow students (who are ready) to vertically stack the numbers and record their work stacked, like the video below. Rory will explain how he did it:

After MASTERING two-digit addition (like in Grade 3!), allow the students to learn the algorithm. At this point, after months of practice, the algorithm will make sense and students will remember the steps because they understand them!!!

E. Practice

Sometimes you just need to practice facts and skills. One of our favourite summer games was: Race to 100! All you need is a 20 sided dice (I think we found ours at London Drugs!), a pad of paper and a pencil.  The goal is to be the first to get to or surpass 100. Here is a score sheet from our last game.

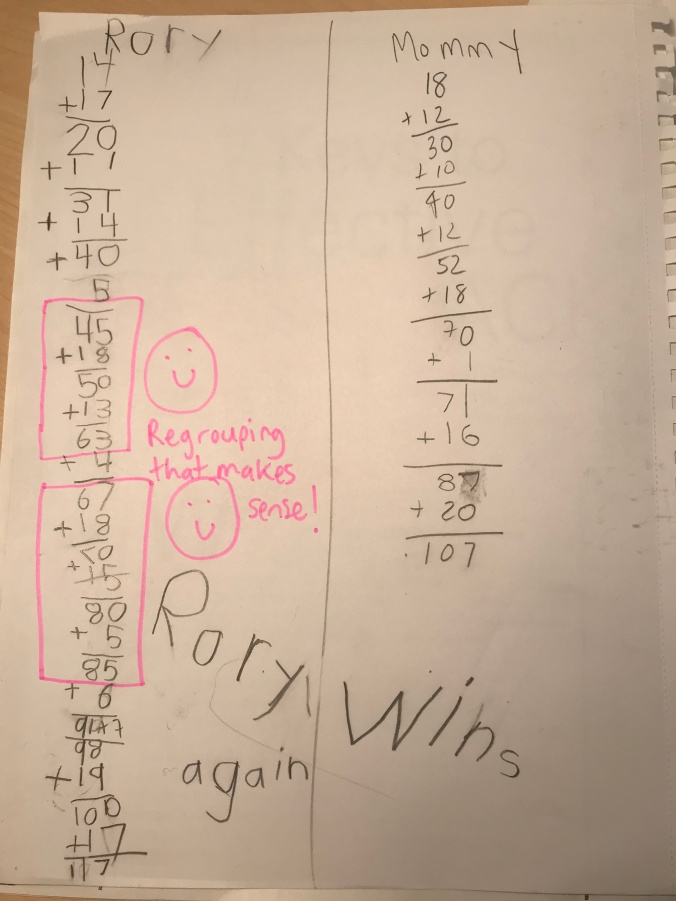
I also believe in teaching addition and subtraction together. This game can easily be reversed (Race to 0!) although I have a different strategy for subtraction…stay tuned!

Have I made you a believer? Are you willing to ditch your original plans for teaching addition or are you already using this method? I hope so!!! If not, write me and I’ll find some more evidence for you!